速算，数学速算方法与技巧（7和8和9三个数字怎么算的63）

数学速算方法有哪些？

第一，充分利用五定律。教师要进行现行教材中运算五定律(加法交换律、加法-组合律、乘法-交换律、乘法-组合律、乘法-分配律)的教学，引导学生搞清楚来龙去脉，不让任何一个学生掉队，培养每个学生自觉使用简单方法，根据不同题型灵活选择简单方法正确快速计算。二、巧用前十后十的方法进行训练。第一个和最后一个十位数法是两个两位数，它们的十位数相同，个位数之和为10。利用两位数与前十位和后十位相乘，乘积的右位刚好是个位数的乘积，乘积的左位刚好是第十位上的数乘以比它大1的乘积，组合起来就是他们的乘积。比如54x56=3024，81x89=7209。第三，注意左右数的组合。任意两位数乘以99或任意三位数乘以999的快速算法称为左右数组合。1.99乘以任意两位数的巧妙计算方法是，从这任意两位数中减去1作为乘积的左两位数，再从这任意两位数中减去100作为乘积的右两位数，这就是他们的乘积。比如62x99=6138，48x99=4752。2.将任意三位数乘以999的巧妙方法是，从这任意三位数中减去1作为乘积左边的三位数，再从这任意三位数中减去1000作为乘积右边的三位数，这就是他们的乘积。比如781x999=780219，396x999=395604。四、利用分数和除法的关系巧妙计算在一个只有两级运算的问题中，顺序计算需要多步计算，利用乘除关系会很容易计算出来。比如24/18x 36/12=(24/18)x(36/12)=24/18x 36/12=4。5.利用膨胀和收缩定律来简化。有些除法题直接计算复杂，容易出错。利用热胀冷缩定律进行合理变形，可以找到简单的解决方法。例如，7/25=(7x4)/(25x4)=28/100=0.28，24/125=(24x 8)/(125 x8)=192/1000=0.192。

常用的速算方法与技巧有哪些？

1.取整法：根据运算的规律和性质，将公式中能取整成整数的部分组合或拆解(尤其是整十、整百等。)，然后得到结果。例如：8 4.1 1 5.9=(8 1) (4.1 5.9)=10 10=20例如：1.2518=1.25(10 8)=1.2510 1.258=12。或者改变运算顺序，或者用归约、加减化简等。例如：4.7 0.25 7.3 4=(4.7 7.3 ) 0.25=3例如：3 4-0.5 0.7-0.3 0.4 5 7=(3 4例如：(1.9-1.90.9)(3.8-2.8)=(1.9(1-0.9)1=0.194。常用数据法：利用一些常用数据，通过数字的等效变形，使计算变得简单。常见数据如：254=100；1258=1000;=0.25=25%;=0.75=75%;=0.8=80%;=0.04=4%以此类推。学生可以自己多列一些，背下来。前面举的例子都应用到这上面了，同学们可以看看。

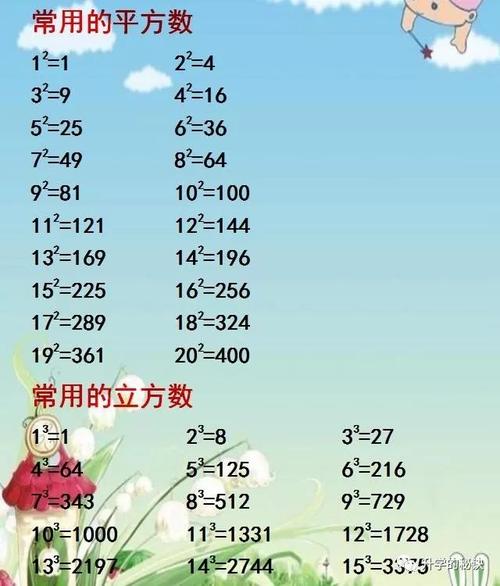
速算法则

1、十几倍一打：公式：头接头，尾接尾，尾接尾。例如：1214=？解： 1 1=1 2 4=6 2 4=8 12 14=168注：乘以一位，如果两位数不够，用0来占位。2.头相同，尾互补(尾之和等于10):公式：一个头加1后，头取头，尾取尾。例如：2327=？解法：2 ^ 1=323=637=21 ^ 2327=621注：乘以一位，两位数不够的用0来占空。3.第一个乘数是互补的，另一个乘数有相同的数：公式：一个头加一后，头乘以头，尾乘以尾。例如：3744=？解：3 ^ 1=4 ^ 44=16 ^ 74=28 ^ 3744=1628注：乘以一位，如果两位数不够，用0来占位。4、几十一乘以几十一：公式：头对头，头对头，尾对尾。例如：2141=？解：24=8 2 4=6 11=1 2141=8615，任意数的11倍：公式：从头到尾不动，中间的和下拉。例如：1123125=？解：2 ^ 3=5 ^ 3 ^ 1=4 ^ 1 ^ 2=3 ^ 2 ^ 5=7 ^ 2和5分别是开头和结尾的1123125=254375。6.任意一个数乘以一打：公式：第二个乘数的第一位不下移，第一个因子的单个位乘以第二个因子后的每一位，再加上下一位，然后往下掉。例如：13326=？解：13位是3332=11 326=12 36=18 13326=4238注：数超过十时要输入一。扩展数据：选择72是因为它的因子更多，容易整除，计算更方便。它的因子是1，2，3，4，6，8，9，12和它自己。一般利率或期限的复利。

使用72作为分子足够计算一般息率（由6至10%），但对于较高的息率，准确度会降低。低息率或逐日复利对于低息率或逐日复利，69.3会提供较准确的结果（因为ln2约等于69.3%，参见下面“原理”）。对于少过6%的计算，使用69.3也会较为准确。对于高息率，较大的分子会较理想，如若要计算20%，以76除之得3.8，与实际数值相差0.002，但以72除之得3.6，与实际值相差0.2。若息率大过10%，使用72的误差介乎2.4%至−14.0%。较大利息率若计算涉及较大利息率（r），以作以下调整：t = [72+(r-8)/3] ÷ r （近似值）逐日复息若计算逐日复息，则可作以下调整：t = (69.3+r/3) ÷ r定期复利定期复利的将来值（FV）为：FV = PV * (1+r)^t其中PV为现在值、t为期数、r为每一期的利率。当该笔投资倍增，则FV = 2PV。代入上式后，可简化为：2 = (1+r)^t解方程得，t = ln2 ÷ ln(1+r)若r数值较小，则ln(1+r)约等于r（这是泰勒级数的第一项）；加上ln2 ≈ 0.693147，于是：t ≈ 0.693147 ÷ r投资72法则其实所谓的“72法则”就是以1%的复利来计息,经过72年以后,本金会变成原来的一倍。这个公式好用的地方在于它能以一推十,例如:利用8%年报酬率的投资工具,经过9年(72/8)本金就变成一倍;利用12%的投资工具,则要6年左右(72/12),就能让1元钱变成2元钱。参考资料：百度百科-72法则